Further into Backpropagation

In the previous post we applied chain rule(funkily called backpropagation!) to systems with complex functions.In this post we will apply backpropagation to neural networks.In this post we will apply backprorpagation to a two layered neural network.Note that instead of derivation of mathematical formulaes we will focus on intuitive sense of it.We will look to explore implementation of backpropagation with multiple inputs represented in form of matrix of training data.

Lets get started!!!

Consider the network:

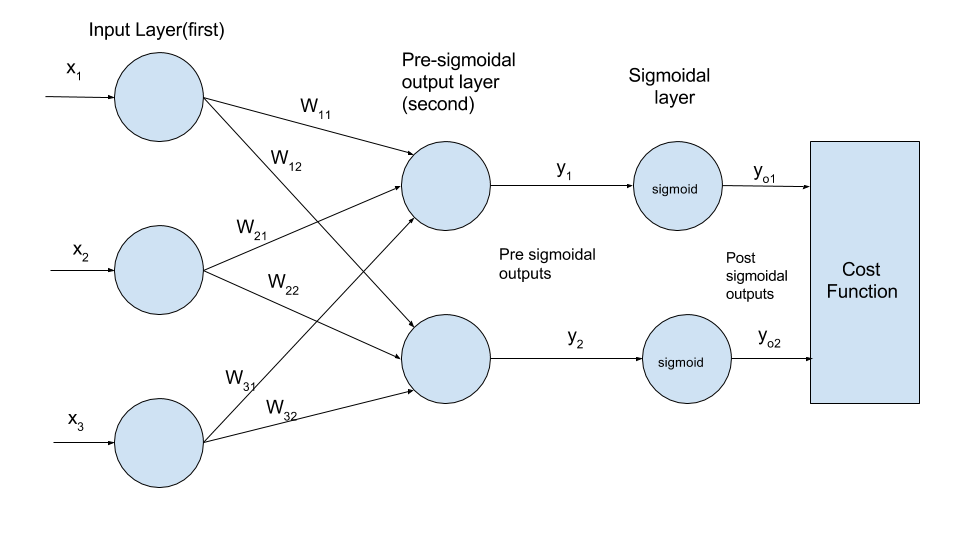
The figure consists of a two layered network.The first layer is the input layer and contains 3 nodes.The second layer is output layer and contains two nodes.In a standard neural network,the sigmoid layer is a part of output layer.For clarity of concept I have drawn it as a separate layer.The sigmoid layer quashes the output values in the range of 0 and 1.The two layers are connected to each other with weights which are represented by edges in the figure.Each node of first layer is connected to every node of second layer.

For those who don’t know how neural networks work here is a short description(Note that this is just a very simple and crude explaination and is sufficient for this post.However,to appriciate the exact mechanism behind it consult other resources too):

The input to the network is pumped through input layer.Here our inputs would be 3 dimensional as there are three nodes in our input layer.These dimensions are also referred to as features.The inputs are multiplied with randomly initialized weights usually in form of matrix.The output of this matrix multiplication is subjected to a sigmoid function.The sigmoidal outputs are used to generate cost function.A cost function is a function that is a measure of deviation of our output from the actual value during the training of network.For this post we will use cross-entropy cost function.The nodes in output layer of our network represent different classes to which the input has to be classified.During the training of network we have a label corresponding to every input.This label represents the true class of that input.

Aim

Our aim would be to adjust the values of weights such that our cost function is minimum(i.e. the deviation of our output from actual value is minimum).

So where do we start?If you are following the posts in series then you would know the answer to this!Thats right!Our update rules.Here we have to manipulate the values of weights to decrease the value of our cost thereby minimizing it.Thus updating weights to decrease the cost:

$$\Large{W_{ij}}={W_{ij}}-h*\frac{\partial C}{\partial W_{ij}}$$

where \(\Large{W_{ij}}\) denotes weight connecting \(\Large{i^{th}}\) node in input layer to \(\Large{j^{th}}\) node in output layer.

We have to somehow find the value of \(\Large\frac{\partial C}{\partial W_{ij}}\) and fill it in our update rule which would decrease the cost function(due to the minus sign).

Now that we know what we desire,lets analyse our cost function \(\Large{C}\).To do this we must first forward propagate through our network to analyse the dependencies of our cost function.Here we would take only one training example which would enable us to appriciate the intricacies better and from there we would extend this to multiple training examples.

Forward Propagation

The training example on which this analysis will be based is \(\Large{x_1},{x_2},{x_3}\) which can be represented in form of 1X3 matrix as: $$\Large{X}=\begin{bmatrix}x_1 & x_2& x_3\end{bmatrix}$$ The weights can also be represented in form of a 3x2 matrix as $$\Large{W}=\begin{bmatrix}W_{11} & W_{12} \\W_{21} & W_{22}\\W_{31} & W_{32}\end{bmatrix}$$ The output before application of sigmoid can easily be found out by multiplying the two matrix to generate a 1x2 output matrix: $$\begin{bmatrix}x_1 & x_2& x_3\end{bmatrix}*\begin{bmatrix}W_{11} & W_{12} \\W_{21} & W_{22}\\W_{31} & W_{32}\end{bmatrix}=\begin{bmatrix}x_1W_{11}+x_2W_{21}+x_3W_{31} & x_1W_{12}+x_2W_{22}+x_3W_{32}\end{bmatrix}$$

Note that the output matrix is a 1x2 matrix with two elements of which one belongs to the first node and other to the second node (of the pre sigmoidal output layer)for a single training example.Let this matrix be represented as: $$\Large{y}=\begin{bmatrix}x_1W_{11}+x_2W_{21}+x_3W_{31} & x_1W_{12}+x_2W_{22}+x_3W_{32}\end{bmatrix}\equiv{\begin{bmatrix}y_1&y_2\end{bmatrix}}$$ where \(\Large{y_1},{y_2},{y}\) are placeholders to facilitate understanding.

Applying sigmoid on this matrix we get:

$$\Large{y_o}=\begin{bmatrix}sigmoid(y_1)&sigmoid(y_2)\end{bmatrix}\equiv{\begin{bmatrix}y_{o1}&y_{o2}\end{bmatrix}}$$ where \(\Large{y_{o1}},{y_{o2}},{y_o}\) are placeholders.

Cost function

\(\Large{y_{o1}},{y_{o2}}\) obtained from forward propagation are used in cost function.Here we are using cross-entropy cost function which is given by:

$$\Large{C}=-\frac{1}{N}\sum_i{p_i*log(q_i)}$$

where \(\Large{i}\) is the number of catagories for classification(equivalent to number of nodes in output unit),\(\Large{p_i}\) is true label of that class and \(\Large{q_i}\) is predicted value and N is total number of training examples.

For this system \(\Large{i}=2\) (as number of nodes in output layer=2 i.e. 2 classification classes).\(\Large q_1=y_{o1}\) and \(\Large q_2=y_{o2}\) as they are the predicted value of the two classes.When we train our network against training data,the label corresponding to a training example would be known.The label represents the class that the training example belongs to.Here let us assume that the training example belongs to the first class.This would make the label values of all other classes to be zero and of the first class as 1.Thus here \(\Large{p_1}=1\) and \(\Large{p_2}=0\).Expanding our cost function for \(\Large{i}=2\),we get: $$\Large{C}=-\frac{1}{N}*(p_1log(q_1)+p_2log(q_2))$$ Putting corresponding values we get:

$$\Large{C}=-(p_1*log(y_{o1})+p_2*log(y_{o2}))$$

Backpropagation

Let us first revisit the matrices that we have: A pre sigmoidal output matrix $$\Large{y}={\begin{bmatrix}y_1&y_2\end{bmatrix}}$$ A post sigmoidal output matrix $$\Large{y_o}={\begin{bmatrix}y_{o1}&y_{o2}\end{bmatrix}}$$ Our weight matrix $$\Large\begin{bmatrix}W_{11} & W_{12} \\W_{21} & W_{22}\\W_{31} & W_{32}\end{bmatrix}$$ Our input matrix $$\Large{X}=\begin{bmatrix}x_1 & x_2& x_3\end{bmatrix}$$

Remember that we had to find the value of \(\Large\frac{\partial C}{\partial W_{ij}}\) to put into update rule which would decrease the cost.We will find this value by applying chain rule as we have done in previous posts but the only difference here will be that we would be dealing with matrices instead of individual variables.While applying chain rule we will focus on the parallelism in dealing with matrices and variables thereby making the transition to matrices smoother and intuitive.

If we look at our network figure and our cost function,we notice that our cost function is a function of \(\Large{y_{o1}},{y_{o2}}\) which is represented in \(\Large{y_{o}}\) matrix which is a function of \(\Large{y_{1}},{y_{2}}\) which is represented in \(\Large{y}\) matrix which is function of inputs and weights.

Let us move back through the system from cost function to input layer and write the chain rule.First we will move back from one node to other and alongside it we will represent layerwise movement in terms of matrices.

• From cost function towards sigmoid layer $$\Large{C}=-((p_1*log(y_{o1})+p_2*log(y_{o2})))$$ We can easily write the derivatives: $$\Large\frac{\partial C}{\partial y_{o1}}=-(\frac{p_1}{y_{o1}})$$ $$\Large\frac{\partial C}{\partial y_{o2}}=-(\frac{p_2}{y_{o2}})$$ We can represent this in form of a matrix: $$\Large\frac{\partial C}{\partial y_{o}}=\begin{bmatrix} -(\frac{p_1}{y_{o1}})& -(\frac{p_2}{y_{o2}})\end{bmatrix}$$

• Through the sigmoid layer- From our experiences in previous posts we can easily write the sigmoid derivatives as: $$\Large\frac{\partial y_{o1}}{\partial y_1}=\sigma({y_1})*(1-\sigma({y_1}))$$ $$\Large\frac{\partial y_{o2}}{\partial y_2}=\sigma({y_2})*(1-\sigma({y_2}))$$ We can represent this in matrix form: $$\Large\frac{\partial y_o}{\partial y}=\begin{bmatrix} \sigma({y_1})*(1-\sigma({y_1}))&\sigma({y_2})*(1-\sigma({y_2}))\end{bmatrix}$$
• Through the pre sigmoidal output layer towards the weights We know the relations $$\Large{y_1}=x_1W_{11}+x_2W_{21}+x_3W_{31}$$ and $$\Large{y_2}=x_1W_{12}+x_2W_{22}+x_3W_{32}$$.From these we can easily find the derivatives: $$\Large\frac{\partial {y_1}}{\partial W_{11}}=x_1$$ $$\Large\frac{\partial {y_1}}{\partial W_{21}}=x_2$$ $$\Large\frac{\partial {y_1}}{\partial W_{31}}=x_3$$ $$\Large\frac{\partial {y_2}}{\partial W_{12}}=x_1$$ $$\Large\frac{\partial {y_2}}{\partial W_{22}}=x_2$$ $$\Large\frac{\partial {y_2}}{\partial W_{32}}=x_3$$

Let us chain all the derivatives elementwise first.Then we will convert it into matrix representation. $$\Large\frac{\partial {C}}{\partial W_{11}}=\frac{\partial C}{\partial {y_{o1}}}*\frac{\partial y_{o1}}{\partial y_1}*\frac{\partial {y_1}}{\partial W_{11}}$$ Putting the respective values we get- $$\Large\frac{\partial {C}}{\partial W_{11}}=\frac{-p_1}{y_{o1}}*\sigma({y_1})*(1-\sigma({y_1}))*x_1$$ Similarly we can write this for all the W’s and place them in a matrix as- $$\Large\frac{\partial {C}}{\partial W}=\begin{bmatrix} -(\frac{p_1}{y_{o1}})*\sigma({y_1})*(1-\sigma({y_1}))*x_1& -(\frac{p_2}{y_{o2}})*\sigma({y_2})*(1-\sigma({y_2}))*x_1\\-(\frac{p_1}{y_{o1}})*\sigma({y_1})*(1-\sigma({y_1}))*x_2&-(\frac{p_2}{y_{o2}})*\sigma({y_2})*(1-\sigma({y_2}))*x_2\\-(\frac{p_1}{y_{o1}})*\sigma({y_1})*(1-\sigma({y_1}))*x_3&-(\frac{p_2}{y_{o2}})*\sigma({y_2})*(1-\sigma({y_2}))*x_3\end{bmatrix}$$ Observe the above matrix.It is nothing but the combination $$\Large{X^T}\times(\frac{\partial C}{\partial y_{o}}\odot\frac{\partial y_o}{\partial y})$$

where \({T}\) denotes transpose of matrix and \(\Large{\times}\) denotes matrix product while \(\Large{\odot}\)denotes element-wise product. Now we can put this expression in our update rule: $$\Large{W}=W-h\ast{X^T}\times(\frac{\partial C}{\partial y_{o}}\odot\frac{\partial y_o}{\partial y})$$The python representation can be given as:

import numpy as np
import random

def sigmoid(x):
	return 1/(1+np.exp(-x))
def derivative_sigmoid(x):
	return np.multiply(sigmoid(x),(1-sigmoid(x)))

#initialization
X=np.matrix("2,4,-2")
W=np.random.normal(size=(3,2))
#label
ycap=[0]
#number of training of examples
num_examples=1
#step size
h=.01
#forward-propogation
y=np.dot(X,W)
y_o=sigmoid(y)
#loss calculation
loss=-np.sum(np.log(y_o[range(num_examples),ycap]))
print(loss)     #outputs 7.87 (for you it would be different due to random initialization of weights.)
#backprop starts
temp1=np.copy(y_o)
#implementation of derivative of cost function with respect to y_o
temp1[range(num_examples),ycap]=1/-(temp1[range(num_examples),ycap])
temp=np.zeros_like(y_o)
temp[range(num_examples),ycap]=1
#derivative of cost with respect to y_o
dcost=np.multiply(temp,temp1)
#derivative of y_o with respect to y
dy_o=derivative_sigmoid(y)
#element-wise multiplication
dgrad=np.multiply(dcost,dy_o)
dw=np.dot(X.T,dgrad)
#weight-update
W-=h*dw
#forward prop again with updated weight to find new loss
y=np.dot(X,W)
yo=sigmoid(y)
loss=-np.sum(np.log(yo[range(num_examples),ycap]))
print(loss)     #outpus 7.63 (again for you it would be different!)

Our cost function decreases from 7.87 to 7.63 after one iteration of backpropagation.Above program shows only one iteration of backpropagation and can be extended to multiple iterations to minimize the cost function.All the above matrix representations are valid for multiple inputs too.With increase in number of inputs,number of rows in input matrix would increase.

My aim for writing this post was to enable you to apply backpropagation to neural networks.Also I wanted you to see the transition between dealing with variables and dealing with matrices.Enough for this time!Enjoy!

Posted on 19 January,2017