Intuitions in Convolutional Neural Networks

In previous blogposts we explored the basics of tensorflow.In this series of posts we will look into different types of neural networks and their implementation in Tensorflow.In this post we will look into the gory details of convolutional neural networks(CNNs) from motivation to reasoning their effectiveness. As we will mostly deal with applying CNNs on images,we will start by looking into digital representation of images and how filters work on an image.We will also look into some theoretical aspects of CNNs which would help us to implement them in coming posts.

Lets get started!!!

Digital representation of images

We all have(hopefully!) drawn pictures on canvas or a sheet of paper at some point in our lives.We would use different colours to accomplish this task.The concept of colour,to most of us,feels pretty abstract.Therefore the representation of images on a screen rather than a piece of paper needed us to express this abstraction in form of a concept.Thus the concept of “pixel” was motivated.

Images are digitally represented in form of “pixels”.These are the building blocks of digital images.You can visualize pixels as tiny rectangles of lights that impart properties to an image.

To further clarify this representation,let us look at concept of resolution.When we state that an image has resolution (2048X1536) we necessarily mean that it has 2048 pixels in width and 1536 pixels in height and thus has total of 2048X1536=3,145,7 pixels or 3.1 megapixels. So a 2X2 image will be made up of 4 pixels which can be visualized as:

The content of these pixels depend upon the kind of image that we are dealing with.Here we will talk about the most common type of image i.e. RGB image.RGB stands for Red,Green and Blue that constitute the primary colours.

In a RGB image,each pixel consists of three channels one each for red,green and blue.Our aim is to use these three colours(channels) in different amounts to generate rest of the colours which would in turn generate the image.To control the colour amount,we divide each channel into something called bit depth.Usually the value of bit-depth is 8.Each of these 8 bit consists value of 1 or 0 and thus the value of channel can range from 0 to 2^8-1 i.e. from 0 to 255.The combination of values from 0 to 255 of these three channels gives the value of a pixel and thus imparts it the resulting colour.For example,the combination (64,224,208) gives the colour Turquoise:

Thus any RGB image of resolution AXB can be represented in 3 dimensions in form of AXBX3 where 3 is the number of channels(Red,Green and blue).Below is representation of a 200X200 RGB image splitted in three channels:

Now that we know basic representation of an image in form of pixels we can move forward to motivate the idea of Convolutional Neural Networks.

Motivating CNNs

Imagine we are given a set of images and their corresponding labels and are asked to come up with a image classification system.What could be the possible approaches?

• One of the straightforward approach can be to come up with a vanilla feed forward network with all the pixels of our image as inputs.In theory this should work wonders as we would have all the information we need to correctly classify the images.But this approach is pretty naive and does not scale well for images with standard resolutions.Lets take an example to understand the problem.Say our input images have resolution 1280X720(which is really a lesser assumption considering todays cameras!).Thus our input images have around 1 million pixels and same will be number of input nodes of our neural network.If we assume that our hidden layer has 10,000 nodes(resonable assumption),the size of our weight matrix will shoot up to 1 millionX10,000 trainable elements!!This is just the first hidden layer!This is pure crazy!!!Thus for even lesser resolution images using a vanilla neural network is computationally too expensive.

• Another approach which can eliminate the problem of expensive computations is if somehow we are able to decrease number of pixels from input image.If somehow we are able to eliminate the noisy pixels from our image and keep only those that are essential for image recognition.We are talking about manual feature selection.Although manual feature selection may prove to be handy in designing of systems such as anomaly detection but while dealing with images it does not help much.You would not know how a network distinguishes between an image of your and your friend’s face.

Thus we can now say that we need a network arrangement that limits the number of parameters and also learns the necessary features by itself.Enter CNNs

Convolutional neural network

Working of a filter

The basic structure of a CNN is a little different from vanilla feed forward neural network.Instead of consecutive layers being fully connected,we introduce the concept of “filters”.When we talk about “filtering” in image processing we are talking about emphasizing or removing certain features.A filter can be visualized as multidimensional matrix of weights.These weights are usually governed by some pattern or principle suitably selected to emphasize or remove features.Filters are usually smaller than our image and are convoluted all over the image.During these convolutions, pixels of our image are modified so as to yield desired modifications in image.Let us make things more clearer with help of an example:

Imagine you are given a 5X5 image and a 3X3 gaussian filter(A filter whose weights are sampled from a gaussian distribution) and you want to apply the filter on the given image.Here “applying filter” is nothing but convolving filter all over the image.

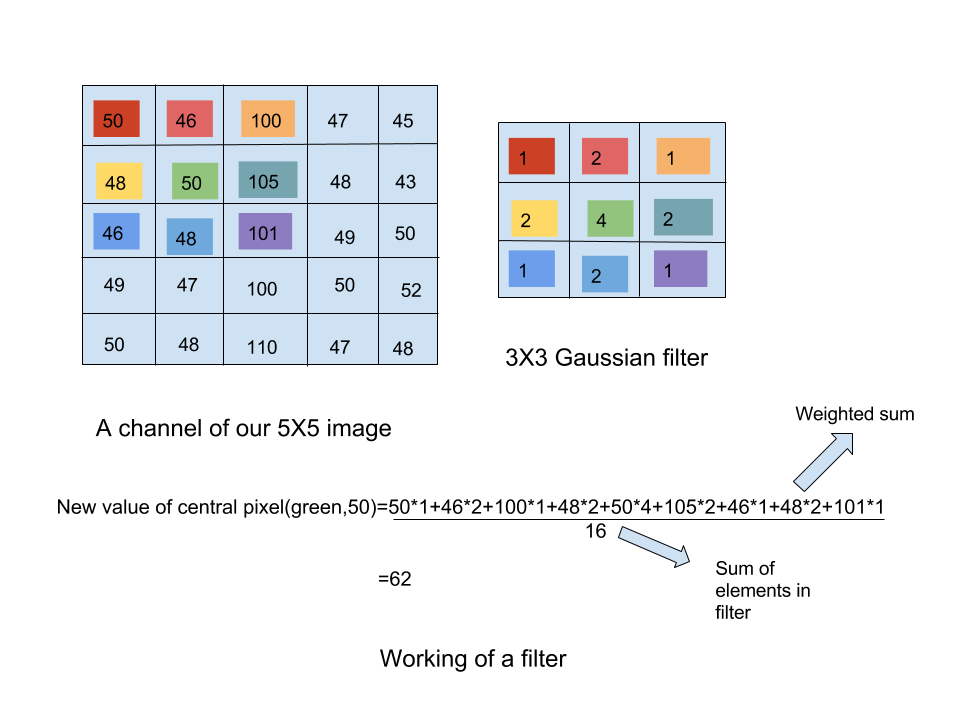
Above figure shows how filter is used to modify pixels of our image.Imagine the filter being placed over our image in such a way that the like coloured numbers in our filter and image coincide.This would mean that (50,green) of our image would coincide with (4,green) of the filter.An operation of weighted mean is carried out as shown in figure.The central pixel(50,green) is modified with the obtained mean value(62).Similarly this operation is carried out by moving the filter such that every pixel of our image gets to be the central pixel(for now neglect the edges when filter would overshoot our image).

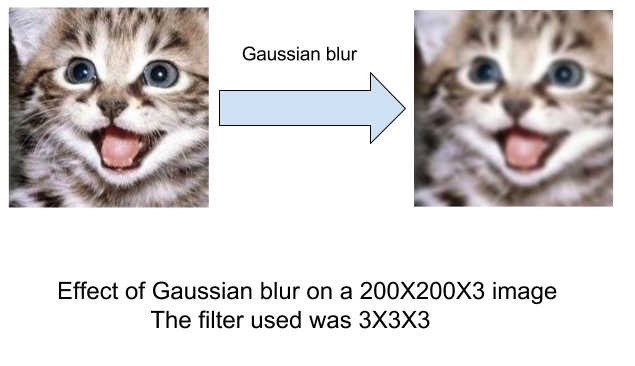
How does the filter affects our image? Different filters have different effect on the image.The gaussian filter is used as preprocessing step in image processing and is responsible for smoothing and removing noise.It leaves a blurring effect.Filters like sobel are used to highlight edges.Thus depending upon their weights,different filters emphasize/remove different features.

CNNs,Finally!!

As the input to a CNN is an image,therefore it operates on volume.The input pixels are stacked in form of volume axbxc where axb is the resolution of the image and c is number of channels(which is 3 for RGB).This is called as input layer.The input layer is subjected to a number of filters to generate activations.These activations along with filters form the second layer of our network(or the first convolution layer).The number of channels in each filter is equal to number of channels in our image.

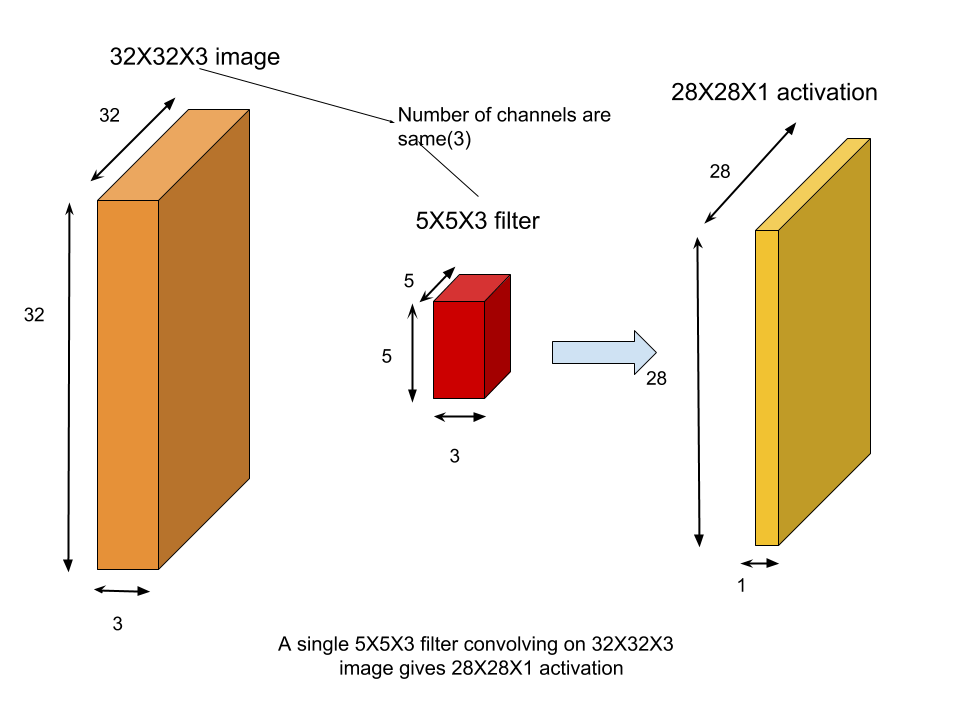
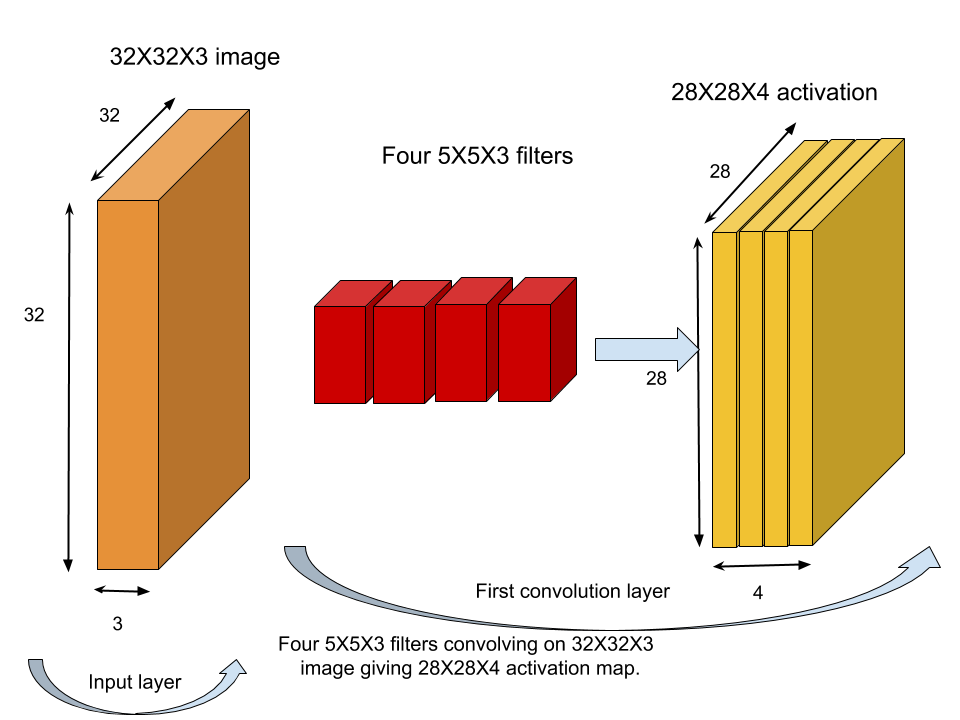
The first of the above two figures shows convolution of 5X5X3 filter on 32X32X3 image.Note that the spatial dimensions of activation map is 28X28.This spatial dimension is smaller because we are only sliding the filter over the image such that it does not overshoots the image.(We will see a concrete mathematical formula to reach to smaller spatial dimension) The second figure shows four 5X5X3 filters stacked to produce four 28X28X1 activations thus giving rise to 28X28X4 activation map.Note that each of the four filters would have access to the input layer and operate directly on our image.

This activation map is passed through a non-linearity(most commonly ReLU).The output is then further exposed to set of filters which will have access to our ReLU applied activation map(and not the input image).To summarize,filters would be applied on the activation of previous layer.We can stack up as many layers as required.Thus the network looks like:

After stacking suitable numbers of convolution layers,we finally connect the activation map to fully connected layer which gives us scores for different classes to be classified.

Trainable parameters

The weights of the filters are randomly initialized.We let our network learn these weights during training.This captures the fact that we let the network decide which features are important for identification of a particular image.Also as filter weights(and biases) and the weights of the last fully connected layer are the only trainable parameters,CNNs have satisfied both the motivations(to decrease number of parameters and feature learning).

Padding

While applying filter to our images,we noticed that their spatial dimensions diminished.This happened because we moved filter only as long as they reached the edge of our image. Thus few pixels at the edges did not get the chance to be at the center of the filter.To visualize this have a look at the figure below:

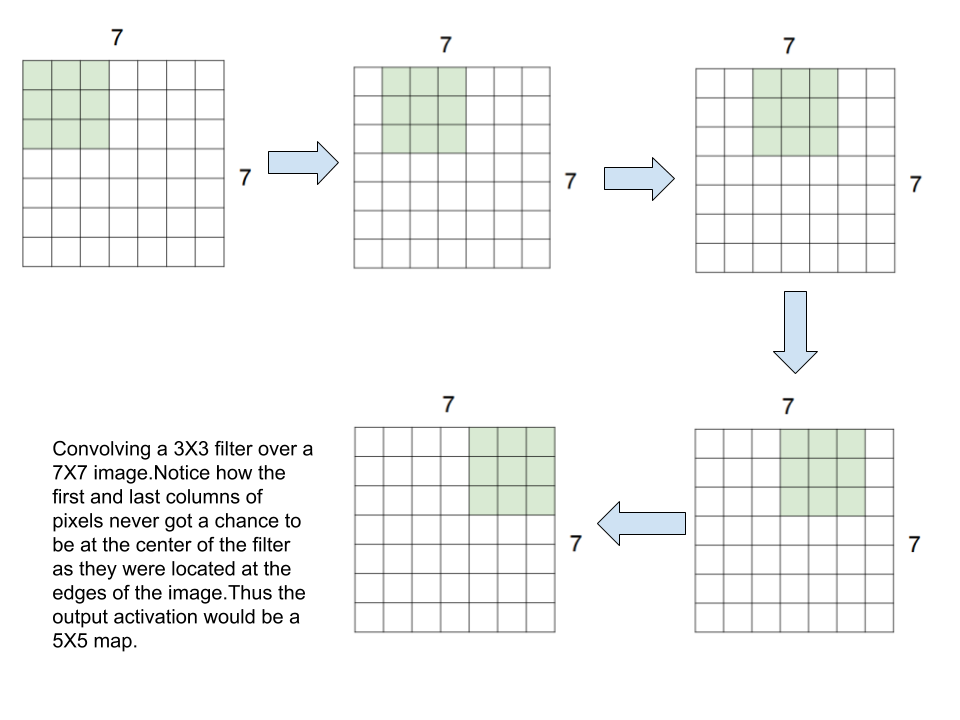
In the above filter convolution as we reach the next state of filter,we move one step towards right.This step is called as stride.In above case stride=1. Although reaching to diminished dimension can easily be visualized in case of small images but for larger ones we need to have a mathematical formula(or not!).The output size is given by:

Output size=(N-F)/stride +1 where N is dimension of input image,F is dimension of filter. 

In this case,N=7 and F=3 so, output size=(7-3)/1 +1=5.

This diminishing of spatial dimensions is undesirable as when our networks gets deep with increase in number of convolution layers,the decrease in spatial dimension would be a problem as it will take away significant chunks of information.To counter this problem,Padding is introduced.

As the name suggests,padding is nothing but padding of images.Our basic problem was that the pixels that were on the edge of our image were left out by the filter.What if they are no more at the edge?This can be made possible by padding our image with zero pixels.This would allow our filter to traverse along the image beyond the edges and thus solve the problem.If we apply zero pad border to our 7X7 example above:

For stride=1,the general formula for number of padding borders required to preserve spatial size of our activation is:

borders=(F-1)/2

where F is size of our filter.In this case F=3,so borders=(3-1)/2=1.

Pooling

Now that we have all the components of our network,we can suggest some modifications to make our network better.To further decrease the number of parameters and to prevent overfitting,we introduce the concept of pooling.Pooling involves downsampling of our activation map.The most common form of pooling used is called max-pooling. Remember that our activation map consisted of individual activations from different filters.Pooling operation is done individually on these activations i.e. pooling operation only modifies the spatial dimension of our activations and leaves the number of activations unaffected.Let us see max-pooling with help of an example:

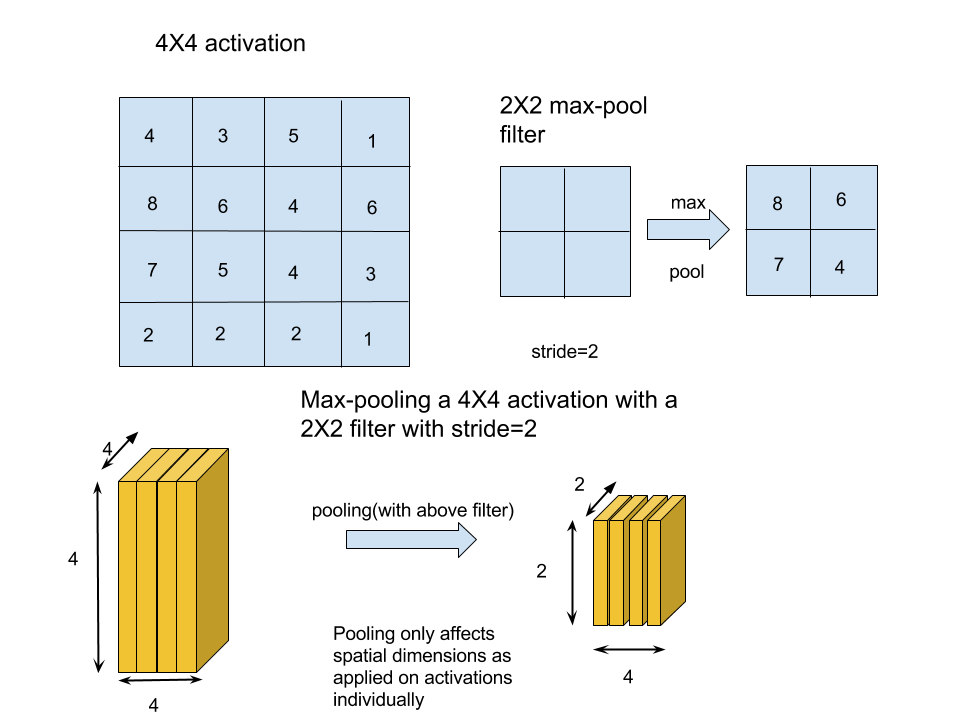
Max pooling is pretty straightforward as shown in above figure.Our 4X4 activation would be traversed by a 2X2 max-pool filter with stride 2.This traversal can be visualized by dividing our 4X4 activation in 4 quadrants.During filter traversal,maximum of each quadrant is preserved and rest of the pixel values are neglected.Thus we get a downsampled max pooled activation. This pooling operation is done after a few convolution layers.In essence the netwok can be viewed as:

Note that the pooling layer is after every second convolution layer.It id just matter of whatever works for you!!!Try different combinations and pick the best for your network.

So this post was all about getting a intuitive feel of CNNs.In the next post we will apply CNNs for image classification task in Tensorflow.Stay tuned!!

Posted on 07 February,2017